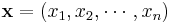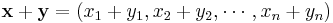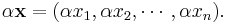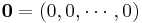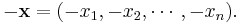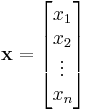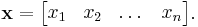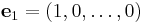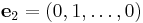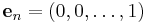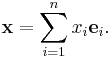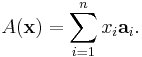Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.
Contents |
Definition
Let F denote an arbitrary field (such as the real numbers R or the complex numbers C). For any positive integer n, the space of all n-tuples of elements of F forms an n-dimensional vector space over F called coordinate space and denoted Fn.
An element of Fn is written
where each xi is an element of F. The operations on Fn are defined by
The zero vector is given by
and the additive inverse of the vector x is given by
Matrix notation
In standard matrix notation, each element of Fn is typically written as a column vector
and sometimes as a row vector:
The coordinate space Fn may then be interpreted as the space of all n×1 column vectors, or all 1×n row vectors with the ordinary matrix operations of addition and scalar multiplication.
Linear transformations from Fn to Fm may then be written as m×n matrices which act on the elements of Fn via left multiplication (when the elements of Fn are column vectors) or right multiplication (when they are row vectors).
Standard basis
The coordinate space Fn comes with a standard basis:
where 1 denotes the multiplicative identity in F. To see that this is a basis, note that an arbitrary vector in Fn can be written uniquely in the form
Discussion
It is a standard fact of linear algebra that every n-dimensional vector space V over F is isomorphic to Fn. It is a crucial point, however, that this isomorphism is not canonical. If it were, mathematicians would work only with Fn rather than with abstract vector spaces.
A choice of isomorphism is equivalent to a choice of ordered basis for V. To see this, let
- A : Fn → V
be a linear isomorphism. Define an ordered basis {ai} for V by
- ai = A(ei) for 1 ≤ i ≤ n.
Conversely, given any ordered basis {ai} for V define a linear map A : Fn → V by
It is not hard to check that A is an isomorphism. Thus ordered bases for V are in 1-1 correspondence with linear isomorphisms Fn → V.
The reason for working with abstract vector spaces instead of Fn is that it is often preferable to work in a coordinate-free manner, i.e. without choosing a preferred basis. Indeed, many vector spaces that naturally show up in mathematics do not come with a preferred choice of basis.
It is possible and sometimes desirable to view a coordinate space dually as the set of F-valued functions on a finite set; that is, each "point" of Fn is viewed as a function whose domain is the finite set {1,2....n} and codomain F. The function sends an element i of {1,2....n} to the value of the i'th coordinate of the "point", so Fn is, dually, a set of functions.
See also
- real coordinate space, Rn
- complex coordinate space, Cn
- examples of vector spaces